Practical exercises with LTSpice
Exercise description
This exercise is designed to familiarize you with the properties of RLC resonant circuits. To do this, do the following exercises.
Exercise 1:
Build a series RLC circuit consisting of:
- resistor ( \(R1=33 \Omega \) ),
- ideal capacitor ( \(C = 10 nF\) ),
- unknown inductor (in the simulation enter L=20mH and \(R_L=30\Omega \) but in further calculations we will assume that we do not know these values).
Then:
- Determine resonance curve (plot I(R1) vs frequency).
- Find central peak frequency (\(f0\)).
- Determine width of the peak (\(Bw\)).
- Calculate Q of circuit: \( Q = f0/Bw \).
- Calculate \(Q_L \)of inductor.
- Calculate inductance L of inductor.
- Calculate series resistance Rs of inductor.
In the next step, measure the amplitude and shape of the signal at the output of a series resonant circuit, when excited with a square wave signal, so that the circuit's resonant frequency is equal to the 1st harmonic of the square wave signal, the 2nd harmonic, and so on up to the 5th harmonic. We can do this by changing the frequency of the square wave signal. If the frequency of the square wave is twice the resonant frequency, the second harmonic will be equal to the resonant frequency, and so on. In this exercise. we can see that an ideal Fourier series of square wave signal consists only of odd harmonics and that the amplitudes of these harmonics decrease like 1/n.
When you're done, compare the result with the video below. Repeat the simulation later for the resistor \( R1 = 130 \Omega \).
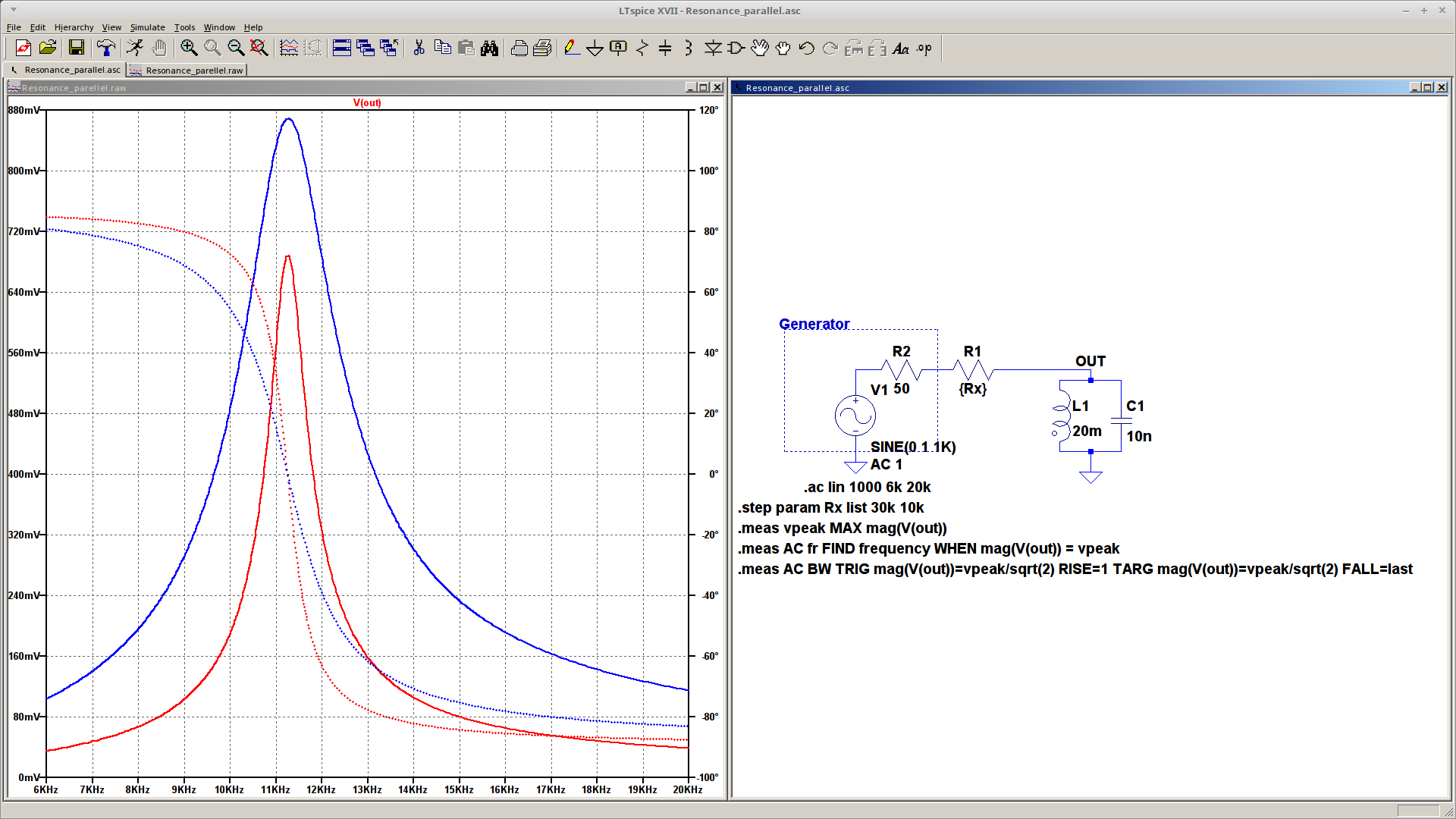
Build a parallel RLC system consisting of:
- resistor ( \(R1=30 k \Omega \) ) and then ( \(R1=10 k \Omega \) ),
- ideal capacitor ( \(C = 10 nF\) ),
- inductor (in the simulation enter L=20mH and \(R_L=30\Omega \)).
Then:
You should get a result similar to the image below: