Theoretical Introduction
Main topics:
- Analysis of diode operation in a circuit with: a constant voltage source, an alternating waveform (small signal) or additional elements in circuit.
- Diode applications
Introduction
The diode is a non-linear element, i.e. its resistance is not constant, but depends on the potential difference across the diode. Despite this, the analysis of the diode can be carried out using, with some limitations, the analysis of linear electric circuits, i.e. by segmental linearization of the diode characteristics.
Analysis of diode operation in a circuit with a constant voltage source:
The analysis of diode operation is usually carried out separately for large and small signals, although it is not possible to precisely determine both. As a guideline (but not a general rule!) the relationship between signals and the diode forward voltage (for a 0.7V silicon diode) can be given: signals smaller by an order of magnitude than this voltage (several tens of millivolts and less) can be considered small and for such signals the diode is treated as a linear element with resistance \(r_d\) (see below), and for signals comparable to and greater than this voltage, the diode is a non-linear element, and its characteristics can be approximately described by a curve - "broken". Such an approximate description of the properties of non-linear elements is characteristic for a quick, though not very accurate, analysis of the operation of systems with diodes operating in such conditions.
Let's analyze the operation of a diode in the circuit shown below, consisting of: a voltage source \(E\), a resistor \(R\) and a diode \(D\) connected in series. In the presented circuit, the diode analysis is based on the concept of a simple load \( (R) \). According to Kirchhoff's second law, the following equation applies:
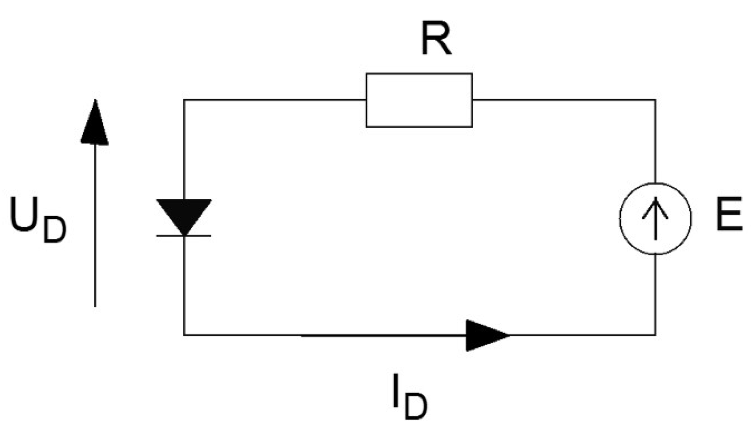
\( E=R \cdot I_D+U_D \) oraz \( I_D =f(U_D) \)
The equation \( I_D = f(U_D) \) can be represented by an exponential relationship (Shockley's equations discussed in the previous lesson) or it can be an experimental characteristic determined independently or supplied by the manufacturer as an average.
Thus, the diode can be analyzed in two ways. The first in a numerical-computer way, and the second in a graphic way, although approximate, but very fast. In the previous exercise, the operating point of the diode was determined using the second method. The above equation is the equation of a line, \( I_D = \frac{E - U_D }{R} \), that intersects the coordinate axes at \(E \) and \( \frac{E}{R} \) and slopes relative to the axis of the system at an angle \( \alpha \) such that \( tan(\alpha) \) is proportional to - \( \frac{1}{R} \). If the values \( E \) and \( R \) are known, and the diode characteristic - curve \( I_D = f(U_D) \) is known, then the intersection of the line corresponding to the resistance \(R \) with the diode characteristic is operating point of the diode \( (I_D, U_D) \).
\( I_D =\frac{E}{R+R_D} \)