Theoretical introduction
Introduction
The aim of the exercise is to familiarize with the transmission of electrical signals in long lines, the basic principles of microwaves propagation in a waveguides and to measure the parameters describing these signals.
In the previously encountered electronic systems (filters, RLC circuits, operational amplifiers, etc.), it was assumed that changes in voltages and currents occur simultaneously in the entire electrical circuit. For example, in the RC integrator (Fig. 1) it is assumed that the same electric currents flow in the resistor R and in the capacitor C at any time.
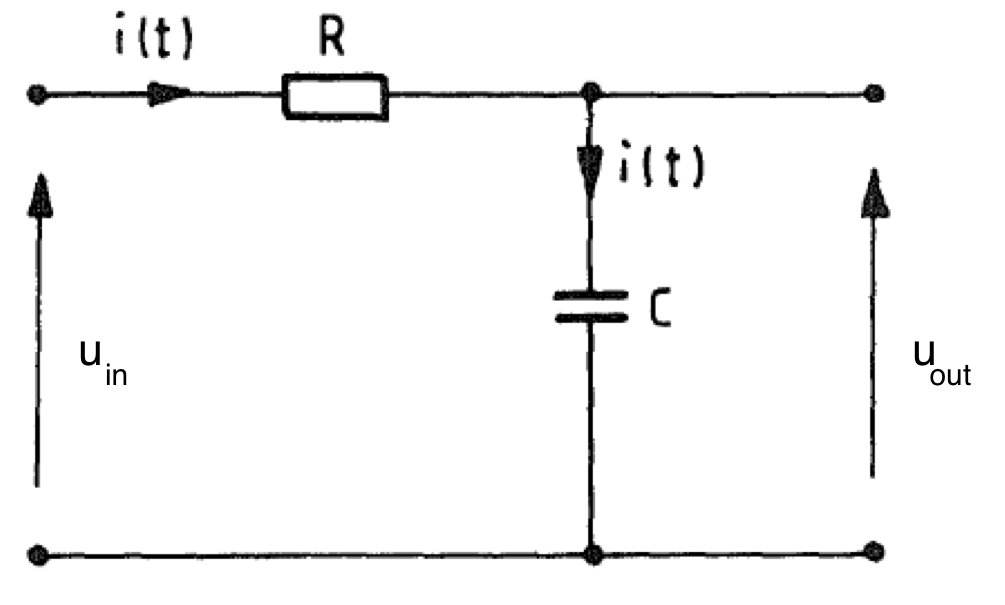
Figure 1
This assumption is valid only when the spatial dimensions of the RC circuit are very small compared to the distance the electromagnetic wave travels during a measurable change in the input voltage \( \Delta U_{in} \) . Thus, the considerations about the circuits discussed so far have only concerned systems whose elements are concentrated in a very small area of space, or to which signals very slowly changing in time are received.
Long lines are such systems of conductors used to transmit electrical signals, the dimensions of which are comparable to the wavelength corresponding to the fundamental frequency of the transmitted signal.
Example
Consider a section of coaxial cable 1 m long, in which the electromagnetic wave travels at a speed of \(V = 2 \cdot10^8 \frac{m}{s}\) (dielectric-filled wire).
(a) When transmitting a signal with a frequency of f=1 kHz:
\( \lambda_1 = V/f = (2 \cdot10^8 \frac{m}{s})/(10^3 \frac{1}{s}) = 2 \cdot 10^5 m \)
Such a system behaves like a system with concentrated constants L and C and can be characterized by capacitance C and inductance L (Fig. 2).
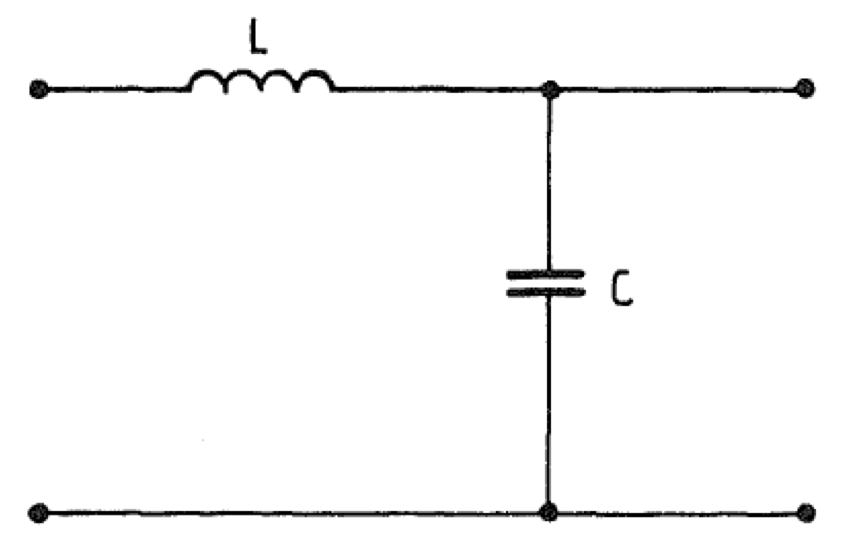
Figure 2
(b) When transmitting a signal with a frequency of f=300MHz:
\( \lambda_1 = V/f = (2 \cdot10^8 \frac{m}{s})/(3 \cdot 10^8 \frac{1}{s}) = 66.7 cm \)
The system behaves like a system with distributed constants.